Viscosity is an important property for understanding the flow behavior of liquids, mixtures, emulsions, slurries and other materials in industrial processes. This one-page reference provides a refresher on conceptualizing viscosity.
Intermolecular forces
Viscosity is a measure of a material’s resistance to flow, and is governed by the strength of intermolecular forces among molecules, as well as by the molecular shapes. In liquids, the internal friction results from stretching and breaking the London dispersion forces between adjacent close-lying molecules of the fluid. Liquid flow only occurs if the molecules are able to move past one another with minimal resistance. Strong intermolecular attractive forces make it more difficult for liquid molecules to move with respect to one another, leading to higher viscosity values. London dispersion forces increase with chain length.
A relationship also exists between viscosity and molecular shape. Liquids with longer, more flexible molecules tend to have higher viscosities than those composed of more spherical or shorter-chain molecules. Longer molecules can also become entangled with one another, making it more difficult for them to move past one another.
‘Two-plates’ model
The two-plates model offers a way to describe viscosity mathematically. Consider two imaginary plates parallel to each other, with fluid between them (Figure 1). If a force (shear force) is applied to the upper plate over a space with area A, while the lower plate remains stationary, the layer of fluid just below the plate moves with it. For the purpose of the model, it is assumed that the fluid sample adheres to the plates, and the flow is imagined to be laminar, in the form of layers of fluid without turbulence.
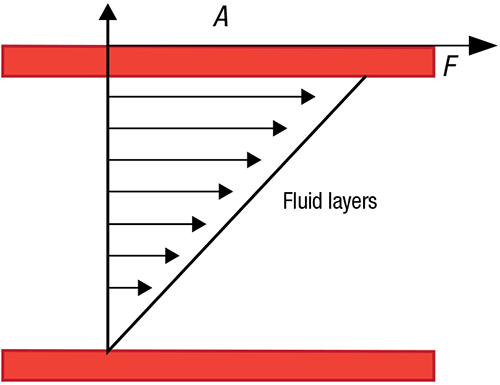
FIGURE 1. A force applied to the top plate will effect shearing in the fluid below
The force required to effect the shearing is known as shear stress, often expressed as the symbol tau (τ). The units of shear stress are Pascals (N/m2). The shear rate ( ∙γ;) is the rate of deformation of the liquid as a result of shear stress). Shear rate (with units of s–1) is thought of as velocity (m/s) over the distance between the plates (h).
Shear stress: ∙γ = F / A (1)
Shear rate: ∙γ = v / h (2)
The ratio of applied shear stress to the resulting rate of shear, Viscosity units are the poise (mPa·s). A related parameter is yield stress, the amount of force required to get a material to begin flowing.
Newtonian vs. non-Newtonian
Fluids that are ideally viscous (Newtonian fluids) have constant viscosity for all shear-rate values (Figure 2). Water and hydrocarbons often exhibit Newtonian behavior. For shear-dependent fluids, on the other hand, the viscosity varies. Because of this, the shear rate at which the viscosity was determined needs to be specified. This is known as apparent viscosity.
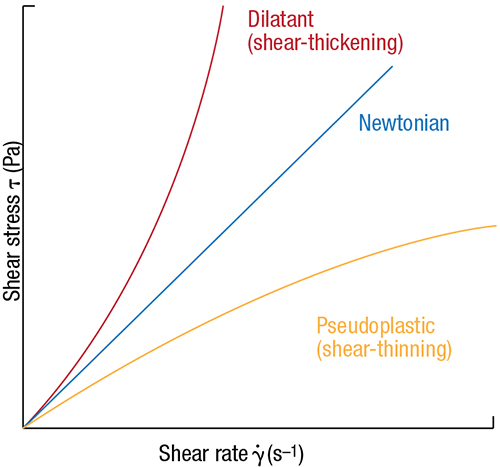
FIGURE 2. Newtonian fluids show constant viscosity for all shear-rate values, while non-Newtonian fluids show divergence
If a fluid’s apparent viscosity is not constant at a given temperature and pressure, but is dependent on flow conditions, such as flow geometry, shear rate and others, then the fluid is said to behave in a non-Newtonian manner. For many industrial applications, expressions of viscosity as a single value fail to capture the full picture of the many factors that affect viscosity. Non-Newtonian viscosity behaviors include the following:
Pseudoplasticity (shear-thinning) occurs when a fluid’s viscosity decreases with increasing shear rate. Many emulsions, polymer melts and solutions, paints, blood and some solid suspensions exhibit this property.
Dilatant (shear-thickening) fluids show increasing viscosity with increasing shear rate. Dilatant behavior is observed in starch suspensions in water, quicksand and in some high-molecular-weight polymers used in drilling muds.
Thixotropy is a situation where a fluid’s viscosity decreases over time under constant shear stress. Clay suspensions used as drilling muds, mayonnaise and some paints and inks behave this way.
Rheopecty refers to a materials that show a rise in viscosity as a result of consistent agitation. Some lubricants exhibit this property, as does heavy cream. A gypsum suspension in water is another example.
A flow curve (rheogram) is a graphical representation of how a flowing material behaves when subjected to increasing or decreasing shear rates (Figure 2). Newtonian fluids have a linear flow curve with a slope intercept at zero. Non-Newtonian fluids have non-linear flow curves and often a non-zero intercept.
References
1. Mezger, Thomas. “The Rheology Handbook,” Hannover, Germany: Vincentz Network, 2020, pp. 108–121.
2. LibreText Chemistry, Intermolecular forces in action, Chapter 11.4, Open Textbook project, 2020. www.libretexts.org.
3. McGregor, R., Viscosity: the Basics, Chem. Eng., Aug. 2009, pp. 34–39.