Chemical engineers who are aware of process control requirements and challenges are in a position to improve process designs
Chemical engineers are ideal candidates for control engineering jobs. They understand processes and process design. However, many have never considered or studied process dynamics. Process engineers often provide the preliminary instrumentation and control requirements for new projects. Control engineering is just the next step. Control engineers try to identify and understand sources of process variability that can impact product quality, and then reduce the variability to mitigate its adverse economic effects.
There are many renowned chemical engineers who have made careers and reputations for themselves as control engineers, including the prolific author Greg Shinskey, the father of model-predictive advanced control, Charles Cutler, and academics like Thomas Edgar, Thomas McAvoy and Dale Seborg.
Even if a process engineer never becomes a control engineer, being aware of process control requirements and challenges will lead to better process designs. This article provides information to aid chemical engineers in their understanding of how to reduce process variability by better controlling processes.
A brief history of process control
Early process controllers were mechanical devices using pneumatics and hydraulics. Mechanical engineers were common in control engineering, especially since the most common final control element — the control valve — is inherently a mechanical device. Pneumatic controllers were gradually replaced with analog electronic systems. Electronics gave the advantage of faster communications between field instruments and controllers located in a central control room, as well as space savings and some improved features. They generally mimicked pneumatic controls, but electrical engineers began to displace mechanical engineers as control engineers. Relay systems were used to provide interlocks, logic control and sequence control.
Inevitably, analog single-loop controllers were replaced with multi-loop digital control systems — first, control computers and later, distributed control systems (DCS). Also at this time, programmable logic controllers (PLCs) began to displace systems of relays for logic and sequential control. Modern control systems are now leveraging the Internet, wireless technologies and bus technologies in new and effective ways. Field instruments and final control devices are becoming increasingly more “intelligent,” providing for more non-control information than control information. Tools and user interfaces are becoming friendlier to use and more capable, offering tremendous productivity gains.
Electrical engineers continued to dominate the field of automation and control. But the additional computing capability in microprocessor- and computer-based systems led to an opportunity for more advanced control strategies. Chemical engineers, with their knowledge of process behavior and process requirements, have been working for years in the field of automation and control, and are often able to gain more value out of control systems than others with less process understanding might achieve.
Design basis and variability
Process engineering focuses on process design, and defines or assumes a design basis. That basis typically includes normal, maximum and minimum production rates, and the process engineer tries to optimize the process design, first in terms of capital cost and second in terms of operability. At this stage, project cost considerations and the availability of standard process equipment may require design compromises that lead to a process design with control challenges.
The design basis is a guideline, but operating conditions in a commissioned plant may change over time. Equipment (especially control valves) wear, feedstock qualities vary, catalysts age, processes are impacted by varying ambient conditions, and other sources of variability impact production. Market and regulatory conditions may also vary, shifting demand for certain products and byproducts or penalizing the production of waste products. The control system of the plant is intended to mitigate the effect of incoming sources of variability on product quality variability. As plants become increasingly complex, operators are faced with bigger challenges, and simply operating the process manually is no longer an option. A frequently cited analogy is the pilot in an advanced meta-stable jet dependent on advanced avionics.
Perhaps the best way to look at automation and control is as the business of managing process variability in real-time. One important thing to understand is that control systems are generally able to attenuate low-frequency (“slow”) variability (on the order of seconds, minutes or more), but cannot attenuate high-frequency (“fast”) variability (less than a few seconds).
Fortunately, process design can often be used to attenuate fast variability. Surge vessels can be used to attenuate highly variable flows between units, for example, reducing the disruption to the downstream unit from variability in the upstream unit.
Control engineers need to understand process dynamics, a topic area that is not always considered as part of the core of process design. It is convenient to think of process dynamics in terms of process inputs and process observations. Process inputs are material or energy flows, and they may be flows into, out of, or intermediate within a given process. As flows are changed, the process is affected, as seen by process observations. Process observations are measured as variables like temperatures, pressures, levels, compositions and flowrates.
As process designs are optimized for energy recovery and minimization of both capital cost and operating cost for a plant, they incorporate increasing integration between process streams. If variability is not controlled in a highly integrated process with a high degree of process interactions, there are more pathways for it to create quality issues. Therefore, it is increasingly important for design and control engineers to work together to ensure operability and strategize how to attenuate variability.
Control basics
Most process responses can be classified into self-regulating and non-self-regulating (or integrating). Self-regulating processes respond to a change in process input by settling into a new steady-state value. For example, if steam is increased to a heat exchanger, the material being heated will rise to a new temperature. Reponses often take the approximate form of first order plus deadtime (FODT) or second order plus deadtime (SODT) (Figures 1 and 2). In a heat exchanger, for example, when the steam valve is opened, more steam enters the heat exchanger. First, the steam pressure in the exchanger rises and heat transfers to the tubes and finally to the colder stream. The temperature of the cold stream takes some time before it begins to rise. Then it rises gradually and increases its rate of change until it approaches the new steady-state temperature, where the temperature rise begins to slow. The characteristic response is a SODT.
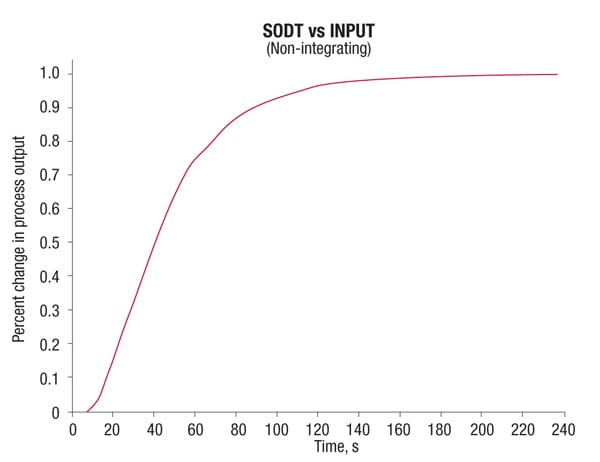
Figure 1. Responses to process inputs in self-regulating processes can take the form of first-order plus deadtime (FODT) or second-order plus deadtime (SODT)
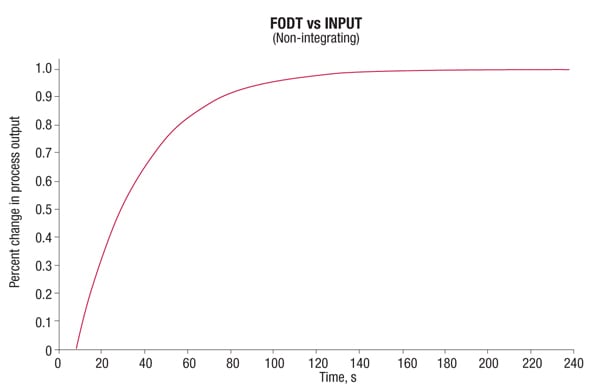
Figure 2. Typical first-order plus deadtime (FODT) responses are characterized by a rapid initial response to a process input, followed by slowing response as a new steady state is reached
The steam flow began increasing as soon as the valve started moving. But if a controller was telling the valve to open, there might have been a short delay before the valve actually moved and the steam flow changed. The steam flow begins to increase quickly and begins to increase more slowly as the new steady-state flow is achieved. This is a typical FODT response.
Self-regulating control loops can be tuned for closed-loop control response to assure that the process observation (sometimes known as the process variable, or PV) is driven to and maintained at its target setpoint. The control response can be tuned for faster or slower response, but as the speed of response increases, so does the risk of overshoot or oscillation.
Different measures of performance have been developed with tuning rules to approximately achieve these objectives. Early performance objectives focused on minimizing error, square of the error, or absolute error over time. Tuning to achieve quarter-amplitude damping was often described in early control literature. Zeigler-Nichols tuning rules were proposed to achieve this kind of response. But this kind of aggressive tuning results in some cycling.
Recent thought in automation prefers to attenuate variability, and that includes closed-loop oscillation, so most loops today should be tuned for a first-order response, with the response time being defined according to process requirements. The fastest-responding loops are limited by the point of critical damping. However, where loops interact, one can be slowed relative to another to prevent the interacting loops from fighting with each other. Important time constants are the deadtime, which is the time before the process observation is observed to change, and a first-order time constant, which is the time it takes once the process begins moving to achieve approximately 63% of the way to the target setpoint. A first-order process normally takes about four time constants, plus the deadtime, to reach steady-state at the target setpoint.
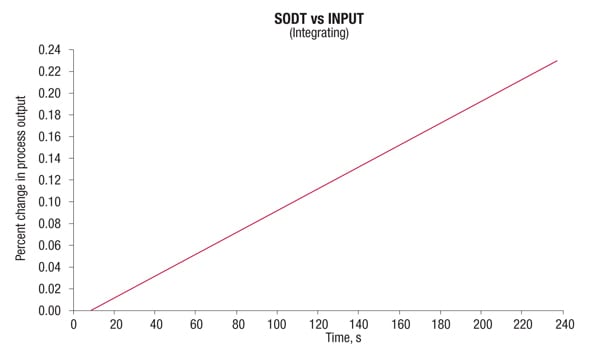
Figure 3. Integrating, or non-self-regulating process variables do not settle into a new steady-state value within allowable operating limits
Non-self-regulating process variables do not settle into a new steady-state value, at least not within allowable operating limits (Figure 3). Changing the rate of feed into a vessel will change the rate at which the level rises (or falls). In the absence of some kind of control, the level would continue to rise until the tank overflowed. Usually integrating process responses can be described as deadtime and integrating gain or ramp rate. Sometimes, there may be a lead or lag associated with the ramp rate, but this is not common, and when it occurs, it tends to be minimal.
Fortunately, controllers can also be tuned on integrating processes to achieve a first-order response. However, the response does not look exactly like the response of a self-regulating process. Following a setpoint change, the PV will move to the new setpoint and overshoot slightly before turning around and settling back at the target value. Following a disturbance, the PV will deviate from the target setpoint until finally being arrested and returning to setpoint. Deadtime is the same as for a self-regulating process. There is no open-loop time constant by definition. However, the closed-loop time constant for an integrating process is defined as the time it takes to first cross the target setpoint following a setpoint change or the arrest time for a disturbance. An integrating process normally takes about six time constants, plus the deadtime, to reach steady-state at the target setpoint following either a setpoint change or a load disturbance.
Feedback controllers
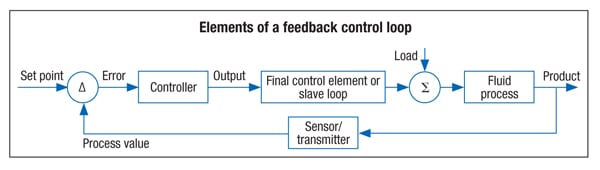
Process control usually takes the form of a feedback controller (Figure 4). Some process inputs can be manipulated in order to drive important process observations to targets or setpoints. Other process observations may not be controlled to a target setpoint, but they are not allowed to exceed upper or lower constraint limits. A control-loop includes a measurement of the process observation to be controlled (the PV), a final control element (usually a control valve) that varies the process flow to be manipulated and a controller that makes a move based on where the process observation is relative to its setpoint.
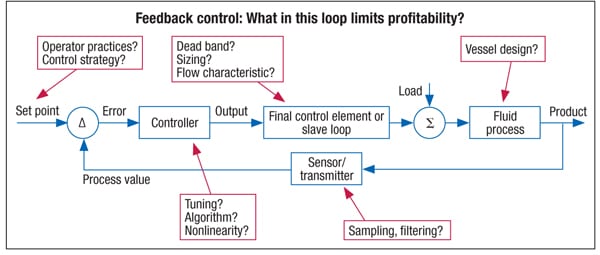
The workhorse controller in the process industry remains the PID (proportional-integral-derivative) controller. It is robust and a good fit for the job as long as the process response is not excessively nonlinear or characterized by a dominant deadtime dynamic. Proportional, integral and derivative are the actions the controller can apply to drive the PV to setpoint. Every controller manufacturer may employ a slightly different form, structure and options, but the functionality and results are the same. The proportional, integral and derivative parameters can be adjusted by the control engineer to provide the best controller response. In order to properly tune a control loop, it is necessary to understand the things that influence loop performance and process profitability (Figure 5).
Often, process inputs can impact more than one important process observation. If the heat exchanger was the reboiler of a distillation column, increasing the steam could affect the levels in the base of the column and the reflux accumulator and compositions at the top and bottom of the column. It might also affect the column pressure and differential pressure, and will affect temperatures up and down the column. Similarly, a process observation might be affected by more than one process input. The distillate composition may be affected by the steam flow to the reboiler, the reflux flow, the feed flow, the product flows and other process inputs. An interactive process requires that the controls be designed to minimize the detrimental impact of multivariable interaction, where two or more loops could fight with each other. One way to do this is with a decoupling strategy, which is something easily understood by process engineers. Feed-forward control and sometimes ratio-control strategies are used to decouple process interactions. The interacting process inputs may be controlled or could be “wild” disturbances. Another way to decouple loop interactions is by tuning one loop for a relatively faster response and the other for a relatively slower response. This technique is very effective and is naturally applied when tuning cascade loops.
Sidebar 1: Tuning a Proportional-Integral-Derivative (PID) loop
PID controllers are defined by the control algorithm, which generates an output based on the difference between setpoint and process variable (PV). That difference is called the error, and the most basic controller would be a proportional controller. The error is multiplied by a proportional gain and that result is the new output. The proportional gain may be an actual gain in terms of percent change of output per percent change of error or in terms of proportional band. Proportional band is the same as gain divided by 100, so the effect is the same, even if the units and value are different. When tuning a control system, it is important to know whether the proportional tuning parameter used in the controller being tuned is gain or proportional band.
When the error does not change, there is no change in output. This results in an offset for any load beyond the original load for which the controller was tuned. A home heating system might be set to control the temperature at 68˚F. During a cold night, the output when the error is zero might be 70%. But during a sunny afternoon that is not as cold, the output would still be 70% at zero error. But since not as much heating is required, the temperature would rise above 68˚F. This results in a permanent off-set.
Integral action overcomes the off-set by calculating the integral of error or persistence of the error. This action drives the controller error to zero by continuing to adjust the controller output after the proportional action is complete. (In reality, these two actions are working in tandem.) The integral of the error is multiplied by a gain that is actually in terms of time. Again, different controllers have defined the integral parameter in different ways. One is directly in time and the other is the inverse of time or repeats of the error per unit of time. They are functionally equivalent, but when calculating tuning parameters, the correct units must be used. Adding further complication, the time can be expressed in different units, although seconds or minutes are usually the design choice.
And finally, there is a derivative term that considers the rate of change of the error. It provides a “kick” to a process where the error is changing quickly and has a gain that is almost always in terms of time. However, again the units of time may be seconds or minutes. Derivative is not often required, but can be helpful in processes that can be modelled as multiple capacities or second order. Derivative action is sensitive to noise in the error, which magnifies the rate of change, even when the error isn’t really changing. For that reason, derivative action is rarely used on noisy processes and if it is needed, then filtering of the PV is recommended. Since a setpoint change can look to the controller like an infinite rate of change and processes usually change more slowly, many controllers have an option to disable derivative action on setpoint changes and instead of multiplying the rate of change of the error, the rate of change of the PV is multiplied by the derivative term.
There are two steps to tuning a controller. First the process dynamics must be identified. This can be done with an open-loop or closed-loop step test. In open loop, the controller is put in manual mode and the output is stepped. The PV is observed and the process deadtime, gain, and time constants are estimated. Several steps should be made to identify any nonlinearity and to ensure the response is not being affected by an unmeasured disturbance. In closed loop, the controller is forced to oscillate in a fixed cycle by stepping the output, forcing it to oscillate with an amplitude that will be dependent on the process gain and step size. This can be achieved with a controller by zeroing the integral and derivative terms and adjusting the proportional gain until the cycle is repeating, or by using logic that switches the output when the cycling PV crosses the setpoint value.
The second step is calculating the tuning parameters. There are different guidelines proposed by different authors and even software that will calculate the tuning parameters for the tuner to achieve the desired response. One guideline that is wisely favored is the “lambda” tuning method. Lambda refers to the closed loop time constant in a controller response. The advantage of this kind of tuning is that the tuner is free to choose the speed of response or the aggressiveness of the controller tuning. There is a tradeoff in loop tuning. As noted earlier, faster response or more aggressive tuning may result in some overshoot or even cycling response that is undesirable and the loop could become completely unstable if there is any nonlinearity in the process. Therefore, robustness is the sacrifice for more aggressive control and lambda can be used to strike an optimal balance between robustness and aggressiveness.
Sidebar 2: Glossary of control terminology
APC – Advanced process control. A general term for types of controls more elaborate than the basic loops. MPC is a type of APC, and MPC is often used interchangeably with APC. Other examples of APC include fuzzy logic and expert systems
ARC – Advanced regulatory control. A complex control strategy often involving more than one PID controller (examples include cascade control, ratio control, feed-forward control, override control and inferential control)
CV – Control variable. A process observation that has a setpoint that may be provided by the operator or by a supervisory controller
DCS – Distributed control system. A digital process control platform in which various controllers are distributed throughout the system
DV – Disturbance variable. Measured process inputs that are not manipulated by the controller (also known as feed-forward inputs)
HC – Hand control. Used to indicate a manually positioned valve
LV – Limit variable. A constraint variable or process observation without a setpoint
MIMO – Multi-input, multi-output. A term describing a multivariable controller
MISO – Multi-input, single output. A term describing a multivariable controller with one output
MPC (1) – Model predictive controller. A controller that controls future error rather than current error. To do this, it incorporates process response models that describe the dynamic behavior of process observations (CVs and LVs) to changes in process inputs (MVs and DVs). This allows the controller to plan moves in the future to provide control over a future time interval. This technology is helpful with processes that have long process delays or a high degree of interaction between multiple process inputs and outputs. It is the ideal platform for constraint optimization
(2) Multivariable process control. Means controlling more than one measurement or variable at a time from the same calculation. Since most model-predictive controllers are also multivariable controllers, the definitions are often used interchangeably
MV – Manipulated Variable. A process input that is an output of a controller
PID – Proportional, integral, derivative. The name used for the most common control loop algorithm seen in the process industries. PID controllers are SISO feedback controllers
PLC – Programmable logic controller. Computer for industrial control
PV – Process value. The term commonly used for the CV of a PID control loop
SIMO – Single-input, multi-output. A term describing an uncommon multivariable controller with one process output (an example would be split-range control)
SISO – Single-input, single-output controller. A term describing typical PID controller or any controller with one input and one output
SP – Set point. The target value for the control variable
TSS – Time to steady state. The time required for a self-regulating process to come to a new stable steady state after a change to a process input
Advanced process control
There are different definitions of advanced process control (APC). Some people consider ratio control and override control to be advanced control. Control strategies that use feed-forward, override-control, cascade and ratio loops and other complexities are often referred to as advanced regulatory control (ARC). Another type of controller is the multivariable, model-predictive controller (MPC). The response models of all process outputs to changes in any process inputs are modelled and incorporated into the controller.
The controller attempts to maintain the controlled variables at targets and constraint variables within limits while minimizing the moves of process inputs. It does this with an algorithm that controls a prediction sometime in the future rather than the current process value. It is an ideal approach for interactive problems, since instead of decoupling the interactions, it coordinates the moves to compensate for or accommodate the known interactions. Those interactions are identified in the embedded models. It is also the only truly effective means of handling deadtime-dominant processes because the deadtime is inherently defined in the controller models.
APC has been widely applied in the petroleum refining industry and is gaining greater acceptance in other industries. It is an excellent platform for constraint optimization. Many process-control problems benefit from constraint optimization. Optimization objectives, such as maximizing production and yield, and minimizing give-away and energy consumption are examples of where constraint optimization can generate substantial benefits over single-loop control. Maximizing or minimizing some variables can drive the process to constraint limits and the models allow for tight control at constraint limits without violating them (Figure 6).
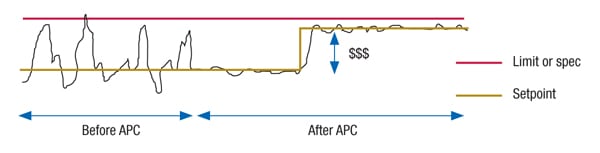
Figure 6. Advanced process control (APC) techniques help allow processes to operate closer to the limit through constraint optimization
Batch process control
Up to this point, the discussion has covered continuous processing. Continuous processes dominate the chemical process industries (CPI), but some sectors of the CPI, including pharmaceuticals and specialty chemicals, rely heavily on batch processing. Some engineers muse that all processes are batch processes, but some batches are longer than others. A batch control engineer might suggest that a batch process is just a continuous process that never gets the chance to reach steady-state. Both are valid points of view. Designing batch process sequences and recipes fall right in the comfort zone for chemical engineers. But the more interesting part of batch control is not defining the normal sequence of steps. Rather, it is defining what should happen when an abnormal event occurs. Can a batch be “saved” following an upset or must it be scrapped? What is required to rework a batch that suffered an abnormal upset? Thinking through the possible problems that could disrupt a batch process and defining safe sequences to abort or recover a batch are classic chemical engineering exercises.
Another opportunity for batch optimization involves trying to minimize transition times between steps. This can be done with equipment selection, but also with logic in the batch sequence. Ramp rates and dwell times can be minimized to the extent practical without impacting batch quality. There is a standard defined (ANSI/ISA S88) for batch process control that standardizes the concepts of control, equipment and unit modules in a batch process.
And batch processes are often designed to make a variety of products or product grades. Furthermore, there may be multiple trains of equipment with some common process equipment or utilities. These plants may involve special recipes. Recently in batch control, the focus has been on managing multiple recipes and optimizing equipment selection for maximum or optimum production.
Because product flaws in the pharmaceutical industry can be devastating, traceability is a major concern. This includes traceability of the materials consumed in the production of pharmaceuticals, and traceability of the equipment and processes used to produce the pharmaceuticals. Regulatory involvement is high, and validation is an integral part of pharmaceutical processes. This requires more data collection and more rigorous adherence to management of change (MOC) procedures than most other processes, whether batch or continuous.
Process safety in control
Another area of process control deals with safety instrumented systems (SIS). Up to this point, the discussion has centered on control requirements to keep the process running in the face of variability. Safety systems have a single function, which is to safely shut down a process if a catastrophe is imminent. Process engineers may be better prepared to consider process safety than most disciplines, at least with regard to the CPI. The general concept is to evaluate the risks, in terms of probability, and the magnitude of the consequences.
Layers of protection are defined and deployed to reduce the risk of a serious safety or environmental exposure. High-risk possibilities need to employ engineering solutions to reduce the risk. Some solutions will include process design, such as dikes around tanks and pressure-relief equipment. Controls will also be employed to reduce the risk, including safety interlocks. The requirement for high on-demand availability of the safety-protection systems leads to specialized safety systems with redundancy (including triple redundancy) and pro-active diagnostics to monitor the health of the safety systems. One of the first layers of protection is alarm management, although it is limited by the presence of the human element to respond to an alarm (for more on alarm management, see Chem. Eng. March 2016, pp. 50–60). Designing safety-instrumented control systems is a specialized area that is critical in managing the risk of hazards in the process. There is a growing trend to design safety systems to be integrated into — but still separate from — the basic control systems. Care is taken during design to ensure the integration does not create a vulnerability or common point of failure of the safety system function and reliability.
Along with this trend is the increasing use of diagnostics and capabilities of “smart” instruments and field devices to reduce the probability of failure on demand. This is a critical consideration for safety systems, because they may not be employed for long periods of time, if ever, but then must work when called upon to shut a process down safely.
Process data
A final area of process control where process engineers can have a significant impact is data management and analysis. Control systems have access to a great deal of data other than control data. Historization and archiving of process data enables process engineers to identify and prioritize continuous improvement opportunities and allows management to make more effective decisions regarding operation and future investment.
Business systems that manage maintenance processes, quality processes, planning processes and other work processes can be integrated with process control. This has been enabled by modern technology for networking, databases, operator interfaces and enterprise-management software all working together. While the nature of integration of these various systems requires more knowledge in computer programming, database administration and networking than chemical engineers might learn in their academic programs, the process management requirements require an understanding of the process plant and its economic sensitivities. Chemical engineers are likely to have a better understanding than most of the information required by company managers at both the local and corporate level in order to make best use of the data and systems in place. The increasing wealth and richness of data makes analysis of that data with evolving “big data” tools a real opportunity. Networking, data sharing, and collaboration between the plant and specialized resources located far away is the promise of the Industrial Internet of Things (IIOT).
Concluding remarks
Often the greatest knowledge gap for a chemical engineer who wants to become a process automation engineer is deep knowledge of instrument and control hardware. This is not an insurmountable problem, however, because vendors are happy to share the information you need. A good salesperson, perhaps contrary to popular opinion, can be a valuable and trusted advisor. The best salespeople know that exaggerating the benefits of one offering for immediate sale may win the order, but will lose the confidence and trust of the customer for future opportunities.
In most cases, vendors truly do want to recommend the most economical solution. To do that, they need to understand the process and control requirements and the expected life cycle of the unit where the offering will be deployed. They can recommend the best measurement technology or valve selection and help size the instrument as well. They can help evaluate the value and return of additional options or choices. So leverage their special knowledge and expertise. Often on a larger project, an engineering firm with its own subject-matter experts may help with selection and procurement, or selection may be defined by corporate guidelines or process licensing requirements.
In the final analysis, the control engineer is trying to identify and understand the sources of variability that can impact product quality, production throughput, yields, utility consumption and other economic impacts, and tries to design controls to attenuate the variability or move it to a part of the process where it has less economic impact. By simply reducing variability, it is possible to operate nearer to constraints and hence maximize the processing capability of the existing plant.
Chemical engineers who are interested in process control can find many resources to gain a deeper understanding in the further reading section.
Edited by Scott Jenkins
Further reading
1. Shinskey, F.G., “Process Control Systems: Application, Design and Tuning,” 4th ed., McGraw Hill, 1996.
2. McMillan, G., “Handbook of Control Engineering,” McGraw Hill, 1999.
3. Blevins, T. and Nixon, M., “Control Loop Foundation – Batch and Continuous Control,” International Society for Automation (ISA), 2011.
Author
 Lou Heavner is a control engineer at Emerson (1100 West Henna Boulevard, Round Rock, TX 78681; Phone: +1 (512) 834-7262; Email: [email protected]). Heavner has been with Emerson for over 30 years, with responsibility for project engineering, sales and consulting with customers across all of the process industries and all over the world. His current role is to scope and lead advanced control and optimization projects, primarily in the oil-and-gas industry. Prior to joining Emerson, Heavner worked for Olin Corp. as a process automation and control engineer. Heavner earned a B.S.Ch.E. degree from the Massachusetts Institute of Technology (MIT) in 1978. When he isn’t helping customers control their processes, Heavner enjoys controlling his own home brewery operation. He may be contacted on LinkedIn at www.linkedin.com/in/louheavner.
Lou Heavner is a control engineer at Emerson (1100 West Henna Boulevard, Round Rock, TX 78681; Phone: +1 (512) 834-7262; Email: [email protected]). Heavner has been with Emerson for over 30 years, with responsibility for project engineering, sales and consulting with customers across all of the process industries and all over the world. His current role is to scope and lead advanced control and optimization projects, primarily in the oil-and-gas industry. Prior to joining Emerson, Heavner worked for Olin Corp. as a process automation and control engineer. Heavner earned a B.S.Ch.E. degree from the Massachusetts Institute of Technology (MIT) in 1978. When he isn’t helping customers control their processes, Heavner enjoys controlling his own home brewery operation. He may be contacted on LinkedIn at www.linkedin.com/in/louheavner.